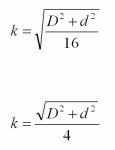Any engineers or engineering students here?

[Jim Oaks]

I have questions about the results I got from this formula for determining maximum stress in a beam supported at both ends and loaded at the center:

[krugford]

General equation for bending stress in a beam is:

Stress = My/I

M = Bending momemt
y = distance from neutral axis (surface (y=c) for max stress)
I = Second moment of area

Z = I/c = section modulus.

If this beam is supported by pins (i.e. heim joint with bolt through it) I would use the beam deflection and moment equations for simple supports because of the small deflections compared to the length of the beam.

Bending moment equation for simple supported, center loaded (point load) beam:

M = Fx/2

x = location on beam up to 0.5* length of beam
F = Applied force

Your equation is the combination of the two I listed. Combining them produces

Stress = Fx/2Z Since it's center loaded x = l/2 So you get:

Stress = Fl/4Z

That the equation for the maximum bending stress in a center loaded simply supported beam. The negative sign doesn't need to be there. It's a sign convention to distinguish between the compression and tension side of the beam, which is usually pretty obvious to determine which is which. Hope this helps.

-krug

[Jim Oaks]

I've done some research on the web and also looked at the Machinerys Handbook.

It's suppose to be understood that all dimensions are in inches, all loads in pounds and all stresses in PSI (except of course metric calculations)

I'm getting (2) yield strength listings for 1020 DOM:

60,000 PSI & 70,000 PSI

and for 1026 DOM I'm getting 70,000 PSI

I did calculations on (4) different DOM tubing dimensions. I used a 5,000lb load applied in the center of a 48" beam. The only part of my calculations I'm concerned about is the l which represents the length of where the tube is supported to where the load is applied. My understanding is that if all dimensions are in inches and I applied the load to the center, than l = 24.

Here are my results:

1.5X.125 (1.5 OD - .125 wall - 1.25 ID)

I = .1284
Z = .1712

5000x24 / 4x.1712 = 175,233 PSI

1.75X.250 (1.75 OD - .250 wall - 1.25 ID)

I = .3400
Z = .3885

5000x24 / 4x.3885 = 77,220 PSI

2.0X.250 (1.5 OD - .250 wall - 1.50 ID)

I = .5360
Z = .5360

5000x24 / 4x.5360 = 55,970 PSI

2.25X.250 (2.25 OD - .250 wall - 1.75)

I = .7962
Z = .7077

5000x24 / 4x.7077 = 42,402 PSI

I don't want to venture off in to shock loads, etc.

My questions are this:

1) Am I corect in using l=24?

2) If yield stress is 70,000 PSI, would my calculations tell me that of the (4) dimensions I've calculated (I know other dimensions exist), the 2.0x.250 DOM would be the minimum size I should choose since the 1.5 & 1.75 are calculating to a PSI higher than the DOM yield of 70,000?


Thoughts?

.

[Dave R]

Originally Posted by Jim Oaks

1) Am I corect in using l=24?

Yes, though I'm curious why your attempting to support the weight of an entire truck in the center of a piece of 4' tubing.

[Jim Oaks]

Well......I'm not. There are different formulas and I'm not sure which one fits best. I'm looking for some type of guide to follow for determining what material to use. Sort of a worse case scenario. If I had a 4-link rear suspension in a 5,000lb truck and stood it up climbing, or went off camber climbing up, I could transfer more weight, but then the weight wouldn't be sitting across the beam, it could almost (thinking as I type.....) be more more of a column supporting weight down through the beam instead of across it.

Next spring I want to start the link suspension on TRS-1 using my Dana 60's. I want to understand how the suspension is measured and set up to function correctly as well as what size tubing and joints to use before I begin. I could easily say 2.5" tubing would work to be safe, but then I'd be adding more weight than was necessary.

[krugford]

Unless I'm looking at something wrong, you should be using l = 48 in.

Stress = Fx/2Z Since it's center loaded, then x = l/2 So you get:

Stress = Fl/4Z

F = Force applied (5000 lbs)
l = length of beam (48 inches)
x = location along beam (max stress for this case is at x = l/2)
Z = Section modulus (you have these)


You're right about the loading you're going to see. You need to use the buckling equations on a 4-Link because the members are going to see axial loading, not bending. The only way you'll see a bending load is if you slip off something and come crashing down on the links. Although the general bending equations would work here, the force applied will be difficult to determine and you'll end up with some pretty hefty links.

Buckling loads are also something I haven't looked at in awhile either....


-krug

[Jim Oaks]

But were talking about applying the force to the middle of the beam that's supported at both ends. So wouldn't it be 24?

48 would double my results giving me a result of 84,805psi on the 2.25x.250 tubing well above the tubes yield of 70,000.

What's the formula for buckling?

Any other engineers or engineering students lurking out there?

[krugford]

The reason you would have used 48" in your equation is because that formala already incorporates the length of the beam divided by two because that formala is specifically for finding the stress at the center of the beam under those loading conditions. It can't be used to find the stress at any other location on the beam. To do that, you would have to de-generalize the equation.

As for the equations for buckling, it depends on what values you have available in your book. A general equation is:

Fcr = (pi^2*E*A)/(l/k)^2

Fcr = minimum critical load
pi = 3.14159....
E = modulus of elasticity (stiffness)
A = area of cross-section
l = length of beam
k = radius of gyration
k = sqrt(I/A)
I = second moment of area (for a tube I = (pi/64)*(Do^4-Di^4))
Where Do and Di are the outside and inside diameters.



You're going to need to know how much force is going to be applied to your links and then find a tube that has a higher minimum critical bucking load, or you could resolve the equation for the outside and inside diameters if you know the force that will be applied. (To do that, you would need a second equation relating the inside and outside diameters, i.e. if you know the wall thickness you want to use). If you're going to this much trouble, I would also do a quick stress calc on the beam from a simple compressive stress viewpoint (Stress = Force/Area), shear calcs on the bolts on the ends, and analyze the loading on the clevis/tabs you'll be using to attach these to the frame and axle.

I have never attempted to design my own 4-link before, although it is something I would like to do. I think that some of the initial loads I would look at would be worst case scenarios. Like if you're climbing a steep hill and stand the truck up on the rear tires, or just one tire, which you've already stated. See how big of a tube that calculates out to. If it's a lot bigger than you normally see on the trail, you may want to re-think. OR you could just have the one truck that won't bend a link on the trail.

And if all this is getting deeper than you wanted, one of my favorite mottos is:

"When in doubt, build it stout"

-krug

[Jim Oaks]

OK.

Been working on some other things..........

Anyways,

I understand what you're saying about using the whole length. I also looked at a picture yesterday in Crawl Magazine of a Jeep standing up trying to climb a ledge. You can see the drivers side rear lower link. It's straight up and down like a column falling more in to a buckling issue at that point.

Let's say my Ranger weighs 5,000lbs and is mostly horizontal. The left rear lower link is resting centered on a rock with the wheel off the ground. To keep things simple we'll say the weight is evenly distributed so that link has 1,250lbs (5,000lbs / 4) on it.

Using the same formula above I would get this:

1.5X.125 (1.5 OD - .125 wall - 1.25 ID)

I = .1284
Z = .1712

1250x48 / 4x.1712

= 60,000 / .6848 = 87,616 PSI

1.75X.250 (1.75 OD - .250 wall - 1.25 ID)

I = .3400
Z = .3885

1250x48 / 4x.3885

= 60,000 / 1.554 = 38,610 PSI

Looking at it that way, The 1.5" tubing would fail because of the 70,000 yield strength and the examples 87,616 PSI calculation but the 1.75" would be fine.

Does it look like I'm calculating that correctly now?

I wonder how you would take the torque applied to the links under accelleration in to consideration?

As far as your equation for buckling:

Fcr = (pi^2*E*A)/(l/k)^2

Fcr = minimum critical load
pi = 3.14159....
E = modulus of elasticity (stiffness)
A = area of cross-section
l = length of beam
k = radius of gyration
k = sqrt(I/A)
I = second moment of area (for a tube I = (pi/64)*(Do^4-Di^4))
Where Do and Di are the outside and inside diameters.

You give the formula for k as k = sqrt(I/A). I've also seen Radius of Gyration for the tubing listed as k = sqrt(D^2 + d^2)/4. When I do both I get different results, so which formula is correct for the tubing. Also, you didn't mention the formula for A (Area of Section). For tubing I have A = pi(D^2 - d^2)/4 or A = 0.7854(D^2 - d^2). Is that correct?

You're going to need to know how much force is going to be applied to your links and then find a tube that has a higher minimum critical bucking load, or you could resolve the equation for the outside and inside diameters if you know the force that will be applied. (To do that, you would need a second equation relating the inside and outside diameters, i.e. if you know the wall thickness you want to use).

What formula are you referring too?

I haven't worked the buckling formula yet.

I find all the math fascinating. I'm dorky like that. I'm surprised some of the other people lurking with engineering knowledge aren't speaking up.

There's not a lot on the net on this, and one chart I looked at didn't look right. I'd rather know how to get the information than rely on what I see on the net.

[krugford]

1.75X.250 (1.75 OD - .250 wall - 1.25 ID)

I = .3400
Z = .3885

1250x48 / 4x.3885

= 60,000 / 1.554 = 38,610 PSI

Yep, that looks right. Long tubes are pretty weak in bending loads like that.

I took my equation for k and plugged in the equations for I and A. I used I = (pi/64)*(Do^4-Di^4) and A = (pi/4)(D^2-d^2) After doing the algebra, I came up with the equation you listed k = sqrt(D^2 + d^2)/4. I put them into excel and got the same answer for k for both equations. Your equation for Area is correct.


As for the loads applied to the links when torque is transmitted to the axle. Those links are going to have to (at a bare minimum) be able to resist the torque at the wheel. I drew a quick four link axle bracket in the image below. Use your crawl ratio to determine engine torque at the wheel.

simplebracket.jpg

Fa = T/(a+b)
Fb = T/(a+b)

Those equations above come from a simple supported beam (the bracket) with a moment load (axle torque) applied somewhere between the supports (the links)

Keep in mind that this assumes that the link is tangential to the torque moment. Since this is an off road truck, the axle is surely going to be below the frame mounts for the links. This means that for the same torque moment, the force on the link will change as the suspension cycles from droop to compression.
If the link is at an angle away from tangential, then the force in the link will be the tangential force divided by the cosine of the angle. In the case of my drawing, the force on the upper link is:

Fupperlink = Fa/cos(Angle a)

The same procedure can be applied to the lower link.

[Jim Oaks]

Krug,

Just to make sure we're on the same page:

k = sqrt(D^2 + d^2)/4

This is:

k = SUM(SQRT((D^2)+(d^2))/4)

The sqrt of (D^2+d^2) and then the sum of that sqrt is divided by 4.

[Jim Oaks]

If the column (link) has a joint at each end, would it be considered a pinned column?

pcr = (pi^2*E*I) / (L^2)